Part B：王为民方程和恒等式

相比大家都很想念王为民了吧，毕竟已经好久没有他的笑料出来了。今天让我们看看他又命名了什么吧

6.8 王为民方程

众所周知，王为民喜欢把一切都加上王为民这个前缀。除了之前捣鼓的王为民版莫比乌斯环外，王为民还捣鼓出了一些数学问题。比如王为民方程和王为民恒等式：

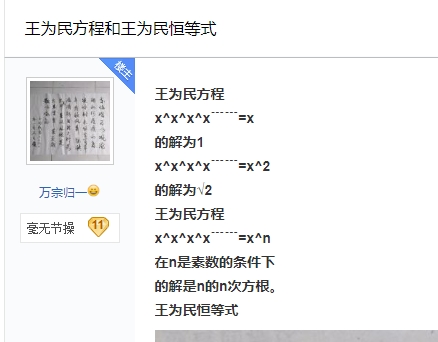
所谓王为民方程，其实就是$x^{x^{x^{x...}}}=x$的解为x=1，其实这就是所谓的迭代幂次，数学上应该表示为$\lim_{k \rightarrow \infty}{^kx}$ 。（例如$^4x=x^{x^{x^{x}}}$ ）。

注意一下，零度君这里犯了一个错误，导致结论出现了问题，无限迭代幂次是有收敛域的。这里给出严谨的证明过程：

1. 定义函数 $f(x)=\lim_{k \rightarrow \infty}{^kx}$，因为涉及到指数和对数，为了方便讨论此处我们暂定x>0。假定函数 f(x)=a 存在，由于 $^{k+1}a=a^{^ka}$ ，可以推出 $a=x^a$ ，显然若a存在必有a>0

2. 构造函数 $g(a)=x^a-a$ ，若 f(x)=a 存在，则必有 $g(a)_{min}\leq0$ 。对于 g(a) 的最小值可以用求导的方式来确定。

3. $g'(a)=x^a\ln x-1$，当 $a=\log_{x}(\frac{1}{\ln x})$时取极小值。显然当a趋向于无穷大和0时， g′(a) 均趋向于无穷大。所以上述极小值也是最小值，即 $g(a)_{min}=\frac{1}{\ln x}-\log_{x}(\frac{1}{\ln x})$

4. 为了方便下一步计算，我们用换底公式对 $g(a)_{min}$ 做一次代换。 $g(a)_{min}=\frac{1}{\ln x}-\frac{\ln(\frac{1}{\ln x})}{\ln x}$ ，显然若 $g(a)_{min}$>0 则 f(x)=a 不存在

5. 做一次换元，令 y=lnx ，则 $g(a)_{min}=\psi(y)=\frac{1+\ln y}{y}$ ，显然y>0，因此当lny>-1时，a不存在。所以为了确保a存在，则必然有 $y\leq\frac{1}{e}$，即 $x\leq e^{\frac{1}{e}}$ 。

6. 同理，当x<1时，可以做类似处理。

7. 综上，当$x\in[ e^{-{e}}, e^{\frac{1}{e}}]$ 时，才存在满足条件 f(x)=a 的a。而王为民方程 $f(x)=x^n$ 也只能在此条件下讨论。

8. 其实王为民的结论是怎么来的呢？既然 $a=x^a$ 存在了，那么当然就有 $x=\sqrt[a]{a}$ 。怎么说呢，零度君觉得王为民估计是看了另一种证明方式。但是那一种方式是用来证明有界的，而不是收敛的。

6.9 迷惑了王为民的另一种证明方法

实际上关于 $f(x)=\lim_{k \rightarrow \infty}{^kx}$的收敛性，网上流传了另一种证明方法，但这个方法是不完善的。方法如下：

1. 定义数列 $a_n=^nx$，其中n为正整数。比如说取 x=2 ，那么 $a_1=\sqrt2$

2. 因为 $a_{n+1}=x^{a_n}$ ，所以 $a_2=\sqrt2^{\sqrt2}<2$

3. 依靠数学归纳法可以证明，当$a_{k}<2$时有$a_{k+1}<2$

4. 所以最终的结论就是 $\lim_{k \rightarrow \infty}{^k2}\leq2$ ，以此来说明这个函数是有界的。

5. 王为民只是将这个方法稍微变化了一点，令 $a_1=\sqrt[x]{x}$ ，那么 $a_2={\sqrt[x]{x}}^{\sqrt[x]{x}}<x$ ，以此证明$\lim_{k \rightarrow \infty}{^k\sqrt[x]{x}}\leq x$

但是零度君说过了，这种方法是有缺陷的。他只能证明有界，不能证明收敛。想要证明收敛性还必须要结合单调性来讲。而最重要的在于，即使证明了收敛性，不代表收敛于多少。所以上面才会有$\lim_{k \rightarrow \infty}{^k\sqrt[x]{x}}\leq x$而不是$\lim_{k \rightarrow \infty}{^k\sqrt[x]{x}}= x$。王为民就是将小于等于写成了等于号。

6.10 王为民恒等式

除了王为民方程外，他还提出了所谓的王为民恒等式，如下图

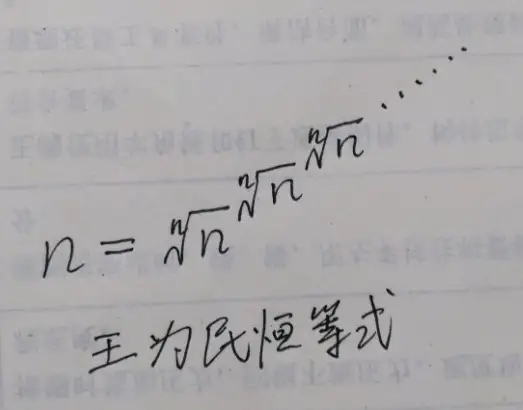
这个其实代换一下就和之前的一样了，就不多说了

6.11 王为民对吧友质疑的回应

实际上这么无脑的问题被吧友拆穿不是什么难事，比如说：

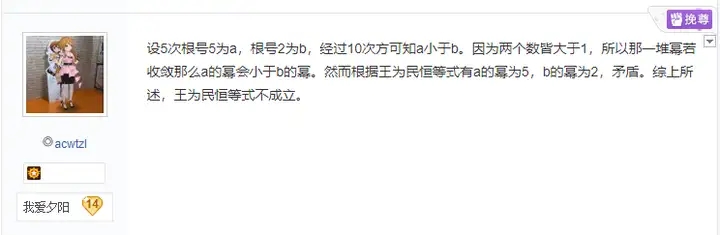
我给大家翻译一下，若定义 $a=\sqrt[5]{5}$，$b=\sqrt{2}$显然1<a<b。那么有$a^{a^{a^{a...}}}<b^{b^{b^{b...}}}$

而根据王为民恒等式，则有$a^{a^{a^{a...}}}=5$，$b^{b^{b^{b...}}}=2$即$a^{a^{a^{a...}}}>b^{b^{b^{b...}}}$

显然，与假设矛盾。因此王为民恒等式是错误的。

王为民是这么回答的......

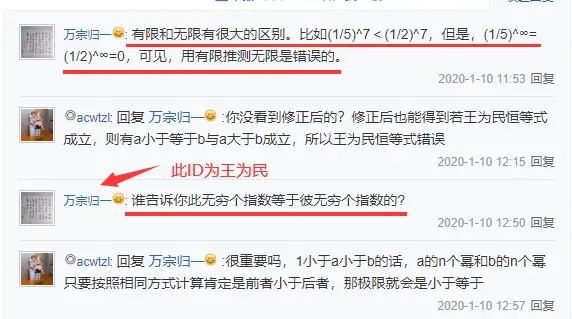
这里零度君替王为民解答一下吧。王为民恒等式确实是错误的，这是因为$\lim_{k \rightarrow \infty}{^k\sqrt[x]{x}}\leq x$而不是等于。我们直接看一下数值结果就知道了。

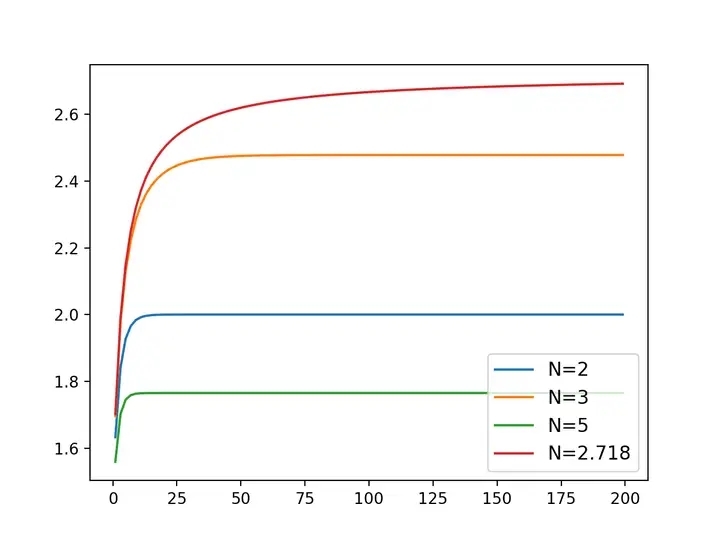
下图中蓝色、橙色、绿色、红色分别代表N=2,3,5和2.718时${^k\sqrt[N]{N}}$随着迭代次数k增大时数值的变化。显然，仅有N=2是一个巧合。而且我们也看到了，其实最起码在x>1时这个函数是当x越接近e时$\lim_{k \rightarrow \infty}{^k\sqrt[x]{x}}$值越大的。

单调性的证明其实很简单，假设 假设 $a,b\in[ 1, e^{\frac{1}{e}}]$且a<b。那么显然有 a<b ，依靠数学归纳法可以证明对任意正整数k均有${^ka}<{^kb}$ ，即${^ka}-{^kb}\geq 0$ 所以有$\lim_{k \rightarrow \infty}{}{^kb}-{^ka}\geq0$ 。故， $\lim_{k \rightarrow \infty}{}{^kx}$ 在 $x\in[ 1, e^{\frac{1}{e}}]$是单调不减的。

但是，函数 $y=\sqrt[x]{x}$ 本身却不是单调的，可以用复合函数求导法得到 $y'=\sqrt[x]{x}\frac{1-\ln x}{x^2}$ ，显然当x<e时单调递增，之后单调递减。因此$\lim_{k \rightarrow \infty}{{^k\sqrt[x]{x}}}$ 在 x∈[1,e] 上递增，在 x∈[e,+∞] 上是递减的。

而王为民恒等式认为 $n=\lim_{k \rightarrow \infty}{{^k\sqrt[n]{n}}}$ ，这个等式的左侧在 n∈R 上递增。显然左右两侧的单调性都不一样怎么可能会是恒等式呢？

6.12 王为民恒等式就是素数公式？

王为民多次宣称他的恒等式就是所谓的素数公式......其实吧......恒等式都不成立哪里来的素数公式

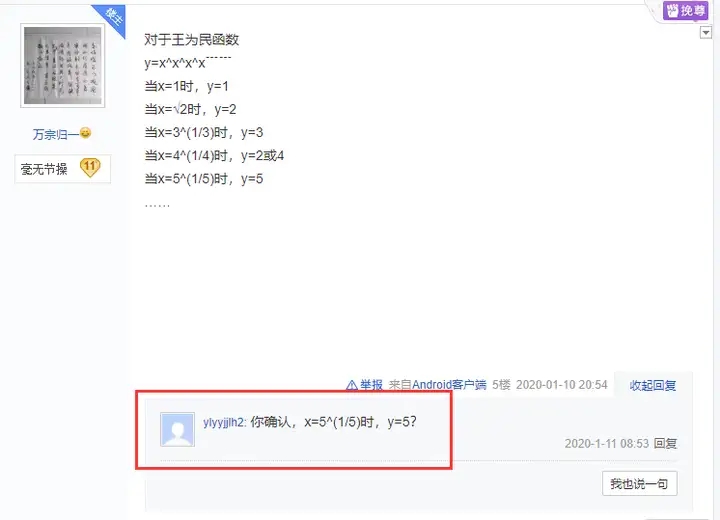
6.13 王为民函数？

实际上王为民之前还把这个所谓的公式叫做王为民函数，只是这面建议王为民重新学习一下算术呢

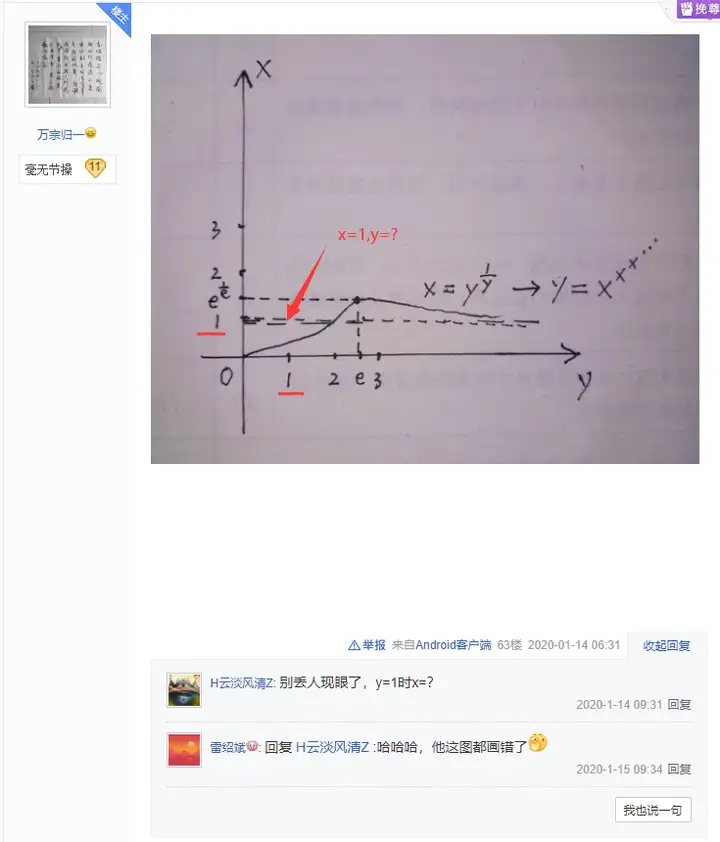
王为民深深的掉入之前的那个坑中，以为$y=\sqrt[x]{x}$就是方程$\lim_{k \rightarrow \infty}{^k\sqrt[x]{x}}= x$的解。还很自以为是的画了函数图像......

这面建议重新建议学一下初中生怎么画函数图像

由于这个函数带有极限，所以标准的函数图像是画不出来的，但是近似的还是可以的。零度君做个好人给他画一下所谓的王为民函数的近似图像吧

方程: $y=^{1000}x$,$x \in (e^{\frac{-1}{e}},e^{\frac{1}{e}})$

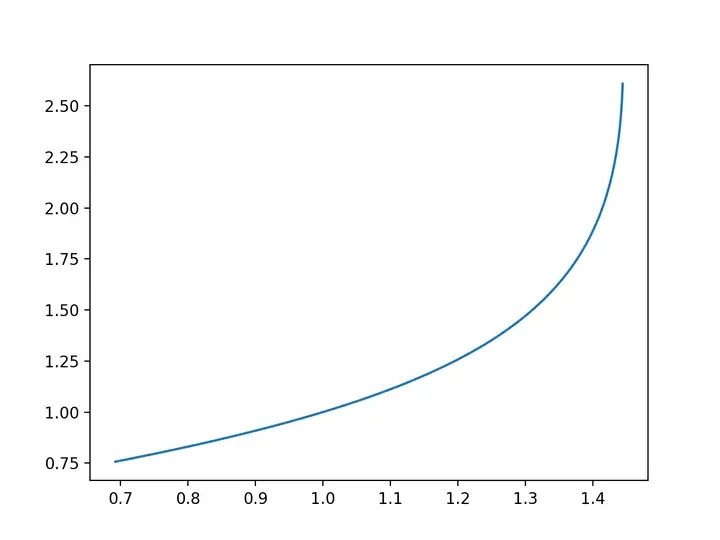
买一送一，再送他另一个吧。

$y=\lim_{k \rightarrow \infty}{^{1000}(\sqrt[x]{x})}$, x∈(0,5) 。另外说一声哦，$x=\lim_{k \rightarrow \infty}{\sqrt[x]{x}}$确实在$x \in [1/e,e]$上成立，不过这也不是什么新鲜事，几百年前就被证明过了。