Part F:雷绍武挑战匀加速直线运动
今天我们找一下老朋友,就是雷绍武雷老师。在最早的几期民科吧见闻录里我们介绍了挑战牛顿力学的雷老师,捎带也介绍了雷老师怒喷匀加速直线运动的事情。但是那时候雷老师没有完整的整理他的理论,今天让我们看一下雷老师最近整理的内容吧。
提示:配合Part-A实用味道更佳呦
2.32 写在最前:速度不是速度
要理解雷老师的理论,我们首先要明白一个精髓那就是:速度不是速度,速度是每秒的位移。你先别急着喷,雷老师定义的速度就是这么回事......为了区分,本文中我们把雷老师的速度定义为雷氏速度。
为了方便理解,我们举个例子:
一个小球初速度为x,运动1s后末速度为y,期间位移为z,那么按照雷老师的定义,1s时小球的速度就是z ......是的,雷老师没法区分瞬时速度和平均速度......(按照物理学通用定义,1s时的瞬时速度是y)
但是我要告诉你,雷氏速度并不是平均速度......因为......雷老师对单位的解释是不一样的。举个例子,1s内运动10m,速度是10 (m/s),不过如果是2s内运动20m那雷氏速度就是20 (m/2s)......
是不是有点绕?没关系,看不懂也不影响接下来阅读
2.33 再战匀速直线运动
我们刚刚说了,雷老师定义的速度其实是每秒的平均速度......所以雷老师就把匀加速直线运动重新定义成下面这样了......我称之为匀加雷氏速度直线运动......
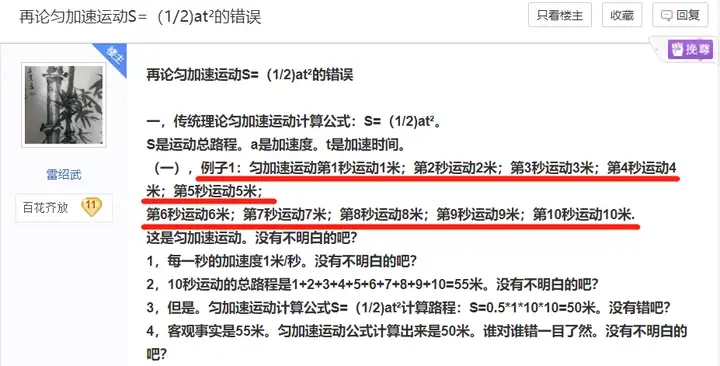

可能你乍一看感觉还挺有道理......匀加速直线运动每秒的位移确实是一个等差数列,而且这个公差确实和加速度在数值上相等(如果是国际单位制的话)......但是,雷老师这第一项他写错了啊......
你还别说,我们看看雷老师的公式就知道怎么回事了......下面就是雷老师提出的运动公式:

我来给大家说一下雷老师这个思路怎么推的:我们都知道匀加速直线运动的平均速度等于首末速度的平均,而时间t时对应的速度为v=at,所以第t秒的平均速度为(假设初速度为0):
这平均速度有了,雷老师的时间单位是1s,那么位移自然也就是:
显然,这是个等差数列,把各项加起来就是总位移:
看到了吧,第t-0.5s和t+0.5s之间的平均速度才是第t秒的......同理,这才是总位移
之前我说过,雷老师把第n秒的平均速度当成第n秒的瞬时速度,所以他的所有计算结果都会在时间上有个0.5s的差异......不信大家可以看看,雷老师的例子2中,如果加速度是5m/s^2,那么......
第0.5~1.5s的位移是5m;
第1.5~2.5s的位移是10m;
第2.5~3.5s的位移是15m;
...
看看是不是和雷老师说的一样啊......
2.34 再战自由落体运动
提起匀加速直线运动,大家自然会想到自由落体运动......雷老师也这么想的:
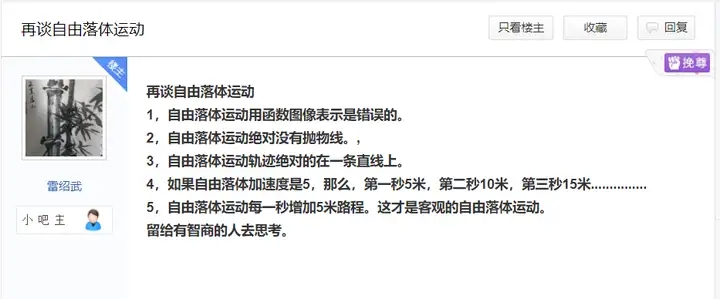
诶等等?按照雷老师的公式去计算的话,重力加速度变成5m/s^2了?这事还要从零度君暴打雷绍武那次说起......Part A:挑战牛顿力学的雷绍武
雷老师亲自去做了自由落体实验,然后为了匹配实验结果把g改成了5......只是改g还是解决不了问题,比如第2s.......
2.35 两球落地重球先?
在贴吧,雷绍武的理论被大家总结为“两球落地大球先”,不过零度君觉得这个总结有点问题,说成两球落地重球先可能更符合雷老师的意思。
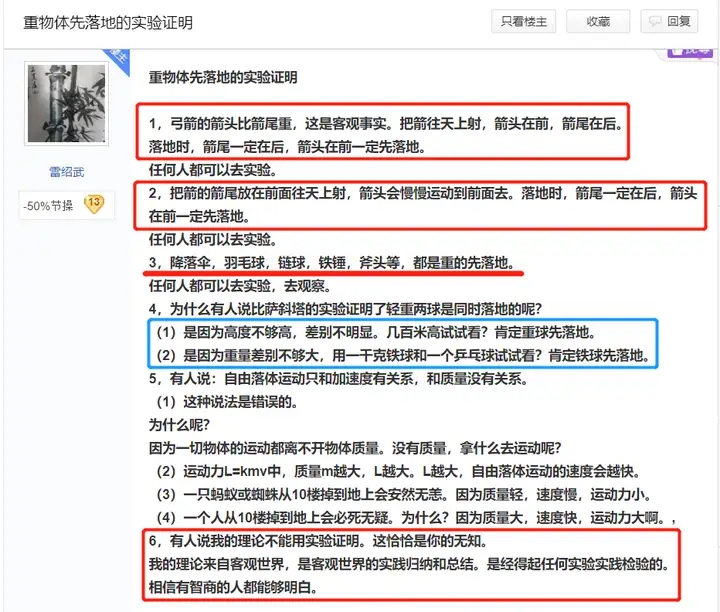
信息量比较大......不过雷老师写的简明直白不需要我再做其他解释......稍微学过物理的同学都知道这是因为空气阻力,有很多逻辑悖论可以拿来玩,比如:

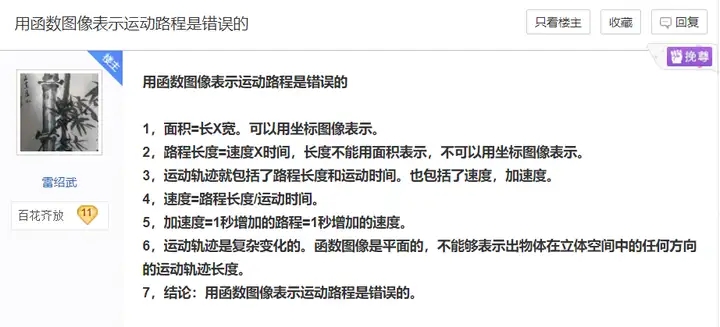
2.36 雷绍武怒喷vt图
高中物理常用vt图来分析问题,所谓vt图就是以时间为横轴以速度为纵轴画的图像。同样的,我们亦可以做出st图像等类似的东西
雷老师可能因为看不懂vt图......愤怒的表示这都是错的......
附录:
其实,雷绍武推导运动公示的方法也不能说完全是错误,错误在于他只会用1秒1秒的思维去考虑问题。即使我们用雷绍武的方式去对到(就公式1中那样),只需要不断缩小误差就能得到结果:比如对于时间间隔△t里,
期间的位移:
累加起来:
显然,只要间隔△t越小越精确,因此取极限之后:
只不过哈,雷绍武的数学能力是理解不了这些个问题的......
Last updated